导函数概述

导函数是微积分学中的一个基本概念，它描述了函数在某一点处的瞬时变化率。在数学分析中，导函数的引入使得我们可以研究函数的局部性质，如函数的增减性、凹凸性等。本文将围绕导函数进行专题练习，帮助读者深入理解和掌握这一重要概念。

导数的定义与计算

导数的定义是导函数的基础。根据定义，如果函数\( f(x) \)在点\( x_0 \)处可导，那么导数\( f'(x_0) \)可以表示为极限： \[ f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \] 这个极限表示了当\( h \)趋近于0时，函数值\( f(x_0 + h) \)与\( f(x_0) \)之差与\( h \)的比值的变化趋势。 接下来，我们通过一些具体例子来练习导数的计算。

例1：计算函数\( f(x) = x^2 \)在\( x = 2 \)处的导数

根据导数的定义，我们有： \[ f'(2) = \lim_{h \to 0} \frac{(2 + h)^2 - 2^2}{h} \] \[ = \lim_{h \to 0} \frac{4 + 4h + h^2 - 4}{h} \] \[ = \lim_{h \to 0} \frac{4h + h^2}{h} \] \[ = \lim_{h \to 0} (4 + h) \] \[ = 4 \] 因此，函数\( f(x) = x^2 \)在\( x = 2 \)处的导数为4。

例2：计算函数\( f(x) = e^x \)的导数

同样地，我们使用导数的定义： \[ f'(x) = \lim_{h \to 0} \frac{e^{x + h} - e^x}{h} \] \[ = \lim_{h \to 0} \frac{e^x \cdot e^h - e^x}{h} \] \[ = e^x \lim_{h \to 0} \frac{e^h - 1}{h} \] 根据\( e^x \)的泰勒展开，我们知道\( e^h \approx 1 + h \)当\( h \)很小时，因此： \[ \lim_{h \to 0} \frac{e^h - 1}{h} = 1 \] 所以，\( f'(x) = e^x \)。

导数的几何意义

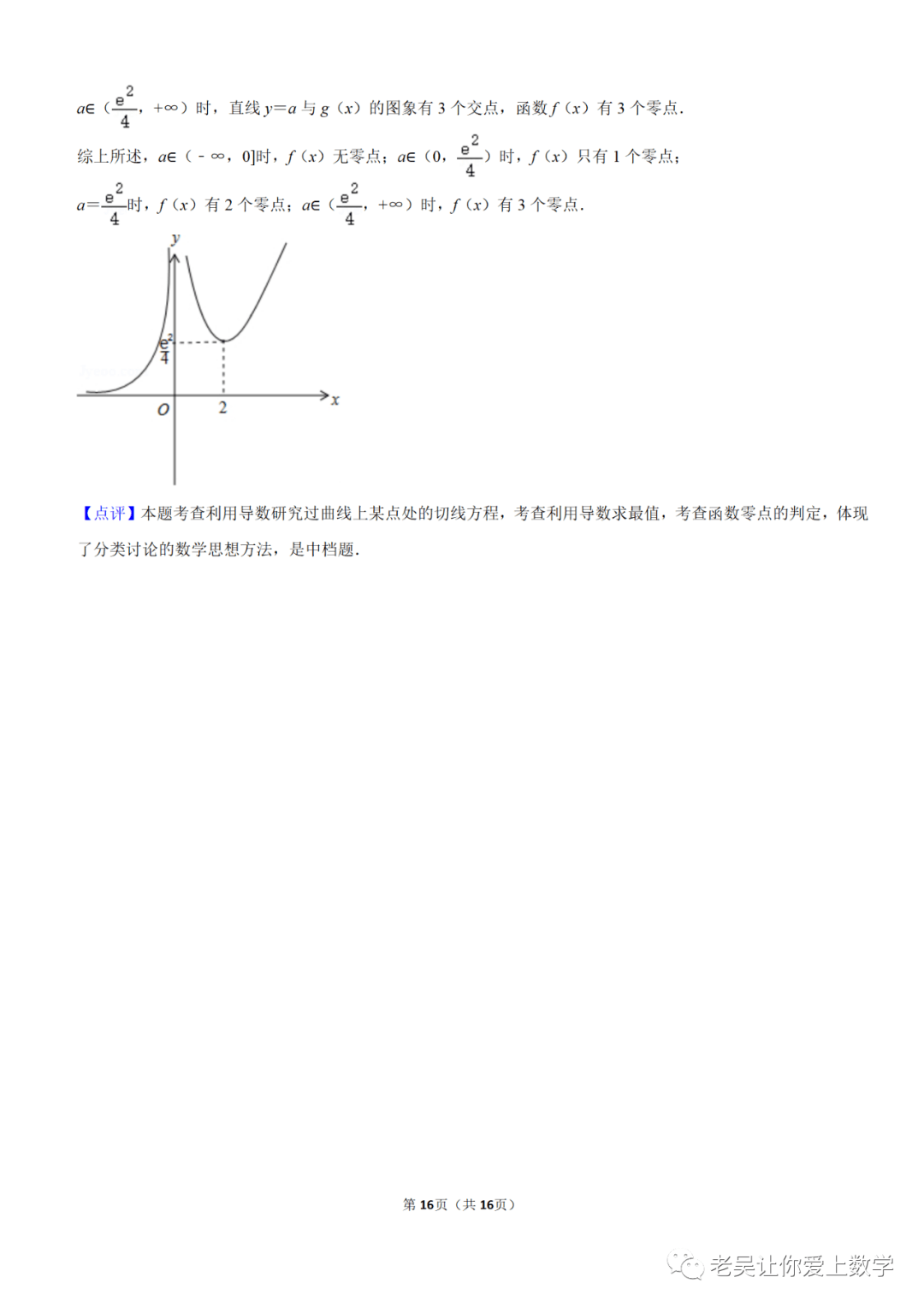
导数不仅具有微分的意义，还具有几何上的意义。在函数图像上，导数\( f'(x) \)表示函数曲线在点\( x \)处的切线斜率。这意味着，导数可以帮助我们了解函数图像的局部形状。

导数的应用

导数在数学和实际应用中都有广泛的应用。以下是一些常见的应用场景： - **极值问题**：通过求函数的导数，我们可以找到函数的极大值和极小值点。 - **函数单调性**：导数的正负可以告诉我们函数在某个区间内是增加还是减少。 - **函数凹凸性**：导数的二阶导数可以用来判断函数的凹凸性。 - **物理应用**：在物理学中，导数用于描述速度、加速度等物理量的变化率。

总结

导函数是微积分学中的一个核心概念，它不仅具有数学上的重要性，还在实际应用中发挥着关键作用。通过本文的专题练习，我们学习了导数的定义、计算方法以及几何意义，并了解了导数在极值、单调性和凹凸性等方面的应用。希望这些练习能够帮助读者更好地掌握导函数这一重要工具。